2つのグループの適切な比較は意外に難しい

経済学、統計学の有力な手法に「因果推論」というアプローチがある。簡単に言えば、2つのグループをより正確に比較するための手法で、効果検証の有効な手段として用いられる。

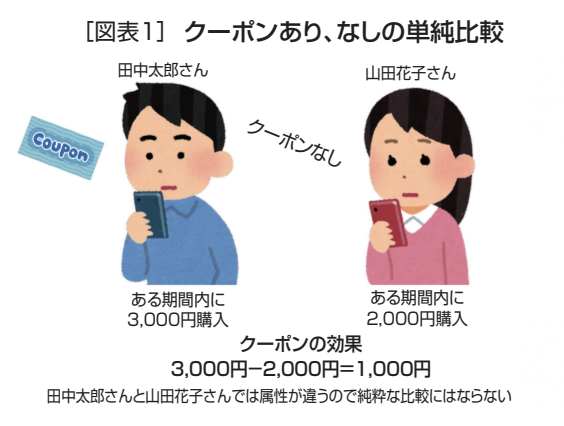
例えば、特典クーポンの効果を知りたいとする。この時クーポンの効果は、それを配ったときと、配らなかったときの2つの状況を比較することでわかる。仮にクーポンを受け取った田中太郎さんは3,000円の購入があり、クーポンを受け取らなかった山田花子さんは同様に1,000円しか購入がなかったとする。この時に、それぞれの売り上げを比較し「3,000円－1,000円だからこのクーポンの効果は2,000円だった」と結論づけたとしよう（図表1）。

これはよく行われる比較の一例であり、一見正しい比較にも見える。しかし、厳密にクーポン効果を測定するなら、“理想的には”クーポンを受け取った田中太郎さんとクーポンを受け取らなかった田中太郎さんを比較することで効果を測定したい。

なぜなら、田中太郎さんと山田花子さんでは、年間購入金額（優良顧客か否か）や価格敏感性（割引を好む、価格には鈍感）、他の販促を受けたか、受けなかったか、クーポン対象商品を前回いつ購入したか、など属性が異なる可能性が限りなく高く、純粋な比較にならないからである。もし山田花子さんが3日前にクーポン対象商品を購入していたら、今回のクーポンの効果が下がるのは当然である。

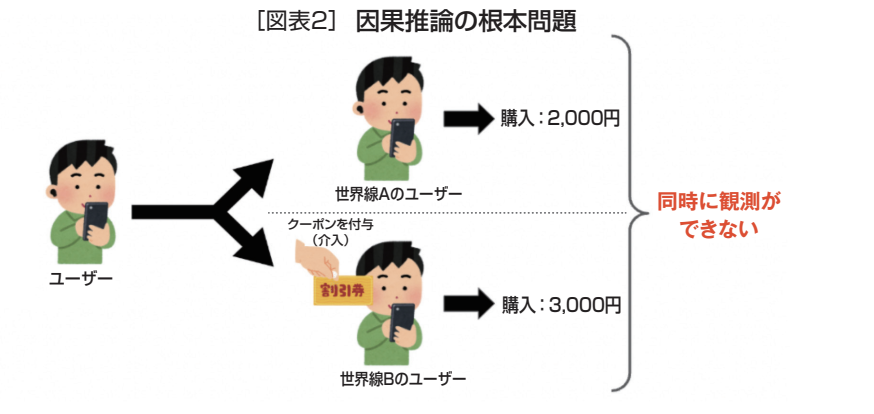
しかし、同じ人で同じタイミングでクーポンのあり、なしを比較することは、タイムマシンでもない限り不可能である。これを「因果推論の根本問題」と言う（図表2）。因果推論とはこのような問題において、なるべく属性の違いを取り除いた純粋な比較を可能にする技術となっている。

データを乱す不正確要素「セレクションバイアス」

単純な引き算では、比較する対象（田中太郎さんと山田花子さん）の属性が違うので、純粋な効果を測定できないことを先に見た。それなら、同じ人を同じタイミングで、クーポンのあり、なしで比較測定すればよいのだが、これはタイムマシンがなければできないことも先述のとおりだ（因果推論の根本問題）。

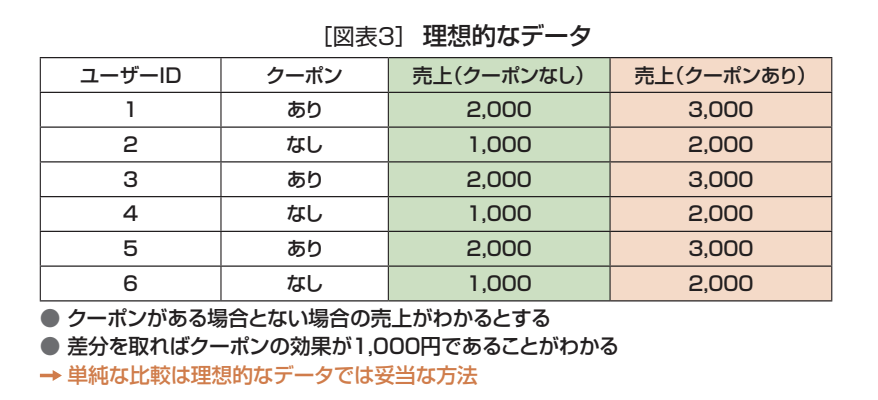
これらの問題を少し補足すると、ユーザーIDごとにクーポンあり、なしで売上を見た場合、図表3「理想的なデータ」では、ユーザーIDごとにクーポンのあり、なしのデータを同じタイミングで取得できるので、その差分が効果になる。しかし、これはあくまで、架空のデータで実在しない（因果推論の根本問題）。

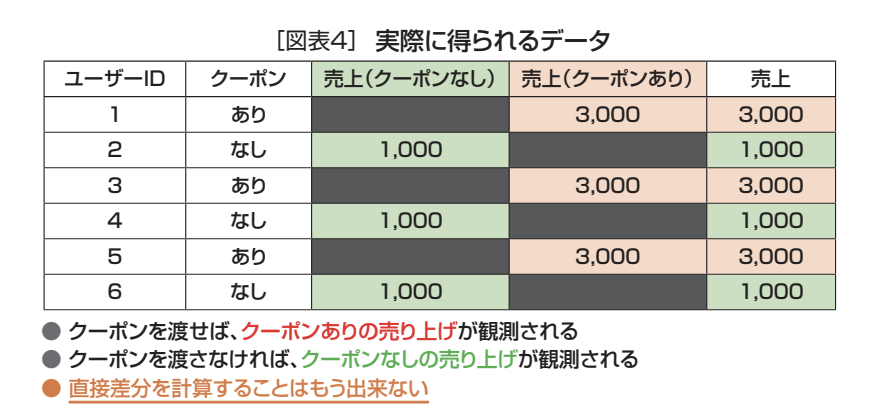
従って、実際に得られるのは、図表4のとおりユーザーIDごとのクーポンあり、なしどちらかのデータとなる。歯抜けデータなので二者間の単純比較はできない。

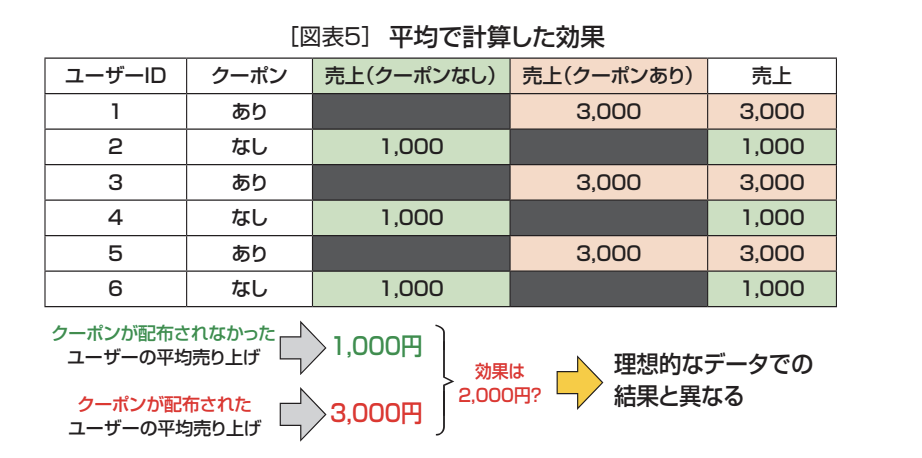
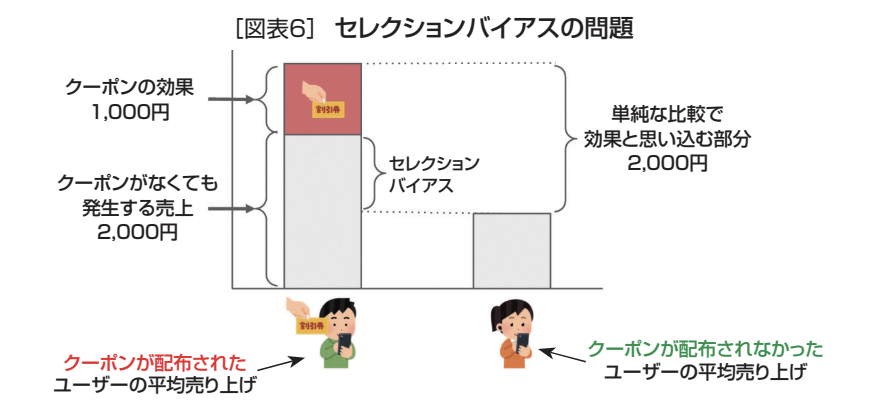
それなら次善策として平均を取って測定してみる（図表5）。しかし、ここでも大きな問題が生じている。それは、クーポン発行者から得た売上の中には、クーポンを発行しなくても実現していた売上の差が含まれているのである（図表6）。

例えば、図表6の例においては、クーポン取得者は優良顧客でクーポンなしでも月間2,000円の買物をしており、クーポンが無いユーザーよりもそもそもの売上が高くなっている。これにより、単純に平均を比較してしまうと、本来の効果よりも大きい効果が推定結果として得られてしまうことになる。これは理想的な同一人物間での比較ではなく、田中太郎と山田花子といった別人の比較を行ったから起きた結果と言える。

このような、施策を打たなくても実現していた効果を「セレクションバイアス」と呼び、これはビジネスで扱うほぼ全てのデータに含まれ得る要素である。小売でよく見られるのは、年間の購入金額が10万円や15万円もある優良顧客へ離反を防ぐため頻繁にクーポンを送るなどの販促を打つことだ。

ここでそのままクーポンを受け取ったユーザーと、受け取らなかったユーザーで売上の平均を比較すると、セレクションバイアスが働いて非常に効果があったように見える。ところが、セレクションバイアスを除去した手法で分析すると販促効果はほぼないことが分かることも多い。

つまり、優良顧客は販促を打たなくても、購入金額は減らないということだ。ムダな販促投資が行われているケースが非常に多い。

セレクションバイアスをいかに除去して、純粋なデータを取るかが正確な効果検証の命運を握っている。

AIを活用して、A/Bテストを擬似的に再現する

ここからは、実際にセレクションバイアスの影響を限りなく小さくした効果検証の方法を見てみよう。まず、施策の対象を「ランダムに」選ぶことができれば、セレクションバイアスが生じないようにデータをとることが可能だ。

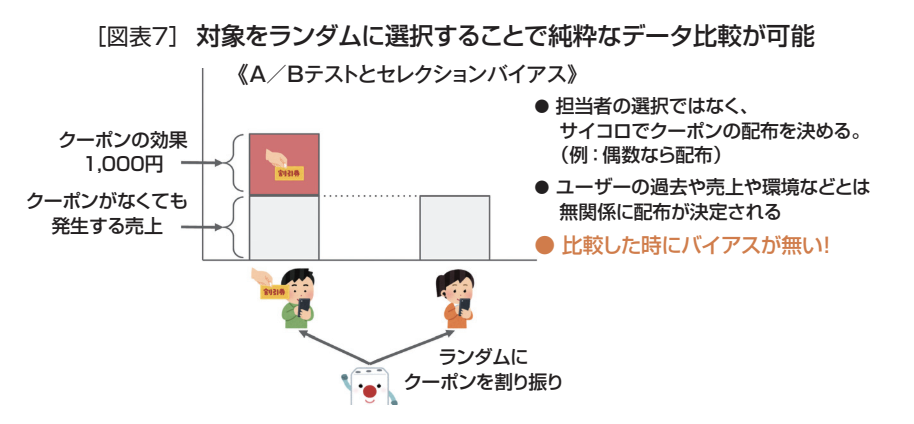
こうすることで、比較する2つのグループ間、例えば、クーポンを発行したグループと発行していないグループ間のユーザー属性もランダムに均等に配分され、比較の中には純粋に効果だけが残る（図表7）。

このように、施策の対象をランダムに選んで2つのグループを比較する効果検証は学術的にはRCT（ランダム化比較試験）といい、ビジネスにおいてはA/Bテストと呼ばれる。

小売業の販促担当者と、このような話をすると、施策をランダムに打つことへ抵抗を示されることが多い。その理由のひとつに、不公平性の問題がある。ランダムなクーポン発行は、もらえる人、もらえない人という差別を生むので、お客への誠実さを欠くのではないかという懸念である。

もうひとつは、ランダムに大量の対象を選び、販促などの施策を届けることは、一定のデジタル技術を要するので、その技術がないという社内事情である。

総合すると、現状小売のリソースでA/Bテストを行うことは非常に困難なので、サイバーエージェントでは、AIを活用してA/Bテストを擬似的に再現することで、より正確な効果検証を実施している。

具体的に説明すると、ある属性を持ったユーザーグループの売上がある（図表8縦軸）。このグループに対して8月、9月、10月にはクーポンを配信せず、11月にクーポンを配信する。このときの効果検証がミッションだったとする。

理想的な効果検証は、先にクーポンを配信したときの11月のデータを検証し、次にタイムマシンで過去に戻り、クーポンを配信しなかったときの11月のデータを検証し両者を比較することだが、これは実際には実行できない（図表8）。

仮にA/Bテストを実施する場合、ランダムに選んだユーザーに対して11月にクーポンを配る事になる。そしてクーポンを配られたユーザーと配られないユーザーの2つのグループを比較することで効果検証を行う。

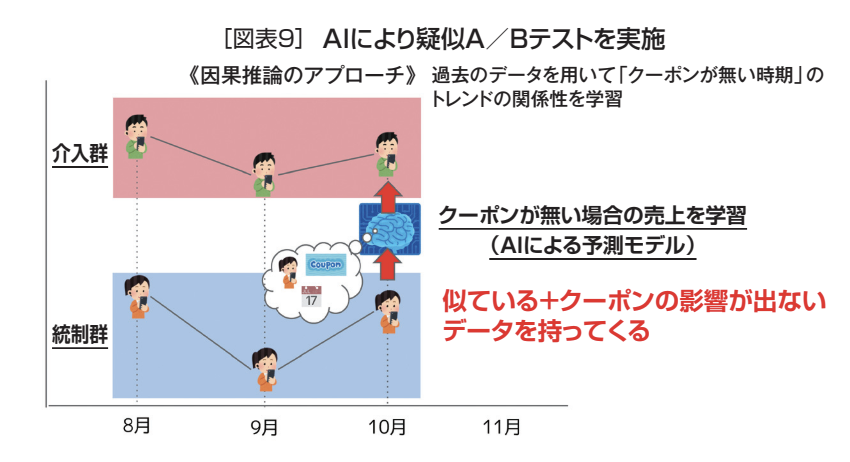
しかし、先述の通り現状では対象をランダムに選び施策を届ける事には様々な問題が存在する。そこでサイバーエージェントの用いるアプローチでは、比較したい対象グループのデータ（図表9の介入群／施策ありのグループ）と類似した傾向を持つデータを別のグループから探し、そのグループのデータ（図表9の統制群／施策なしのグループ）から介入群の売上を予測できるAIモデルを作成する。

例えば、先のクーポンの効果検証を北海道でやるとすれば、それに近い青森のデータを持ってきて、8月、9月、10月の期間において青森の売上データから北海道の売上データを精度高く算出（予測）するAIモデルを作成する。このAIモデルは、青森の売上データを入れると、北海道の売上データの予測結果を返してくれる。そして、それを学習した8月、9月、10月はクーポンが配信されてない時期なので、AIはクーポンがない場合の売上の予測をすることになる。

これにより、青森で11月にクーポンを配信しなかった実績データをAIモデルに入力することで、北海道で11月にクーポンを配信しなかったときの売上を予測することができる。

実際には、北海道では11月にクーポンを配信しているため、AIの予測と実際の売上の差分が効果ということになる。

なお、上記の北海道、青森という地名はあくまで考え方を示した例で、サイバーエージェントでは効果検証をするための統制群（施策なしグループ）のデータをAIが探し出すアルゴリズムも独自に開発している。これにより、より精度の高い効果検証を実現している。

LINEのクーポン効果をAI活用で、より正確に検証する

ここからは、先に見た効果検証手法の実例を紹介しよう。LINEの販促は盛んに行われ一定の効果を挙げている。ここではLINE公式アカウントによる効果検証の実例を紹介しよう。

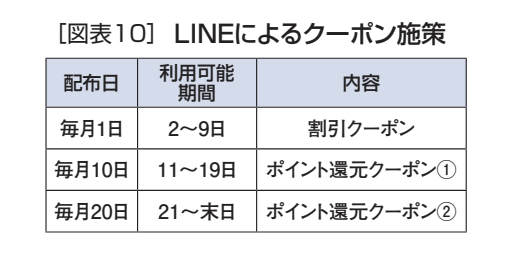
この事例では、図表10で示したように、ある小売業が、友達登録したLINEユーザーに月間に、割引クーポン1回、ポイント還元クーポン2回、計3回のクーポンを配信する。（※なお、割引率、還元率によって結果は異なるが、以降は特定の割引率、還元率での分析結果である）

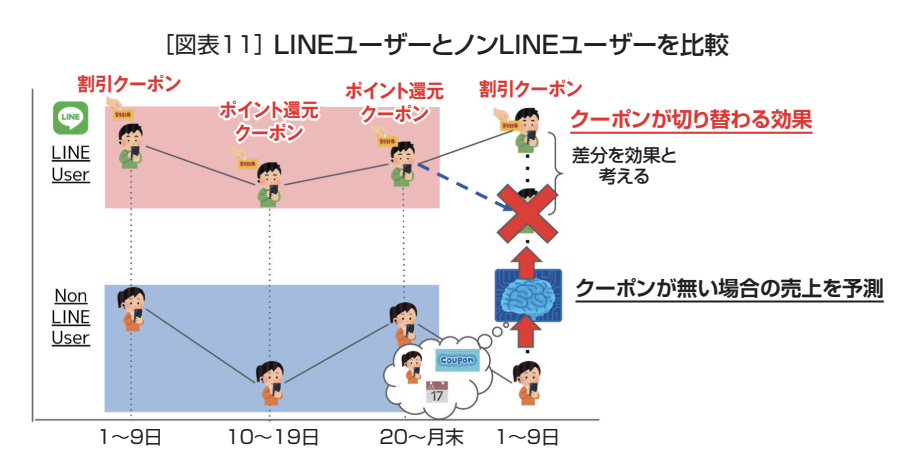
これを月末の2回目のポイント還元クーポンの発行から月初の割引クーポン発行に切り替わるタイミングで購入金額がどの程度変化するかを測定し、割引とポイント還元ではどちらの効果が高いかを検証しようとするものだ（図表11）。

ここではA/Bテストは実施されていないため、友達登録していないNonLINE Userデータを元に算出した予測値を使って効果を検証する。そのために、LINEで友達登録して実際にクーポンを受け取っているLINE Userのグループと友達登録していないNonLINE Userとを比較する。

この事例においては、LINE Userは常に何かしらのクーポンが配信されている状態にある。よって、還元クーポンから割引クーポンへと切り替わるタイミングで分析を行うこととした。

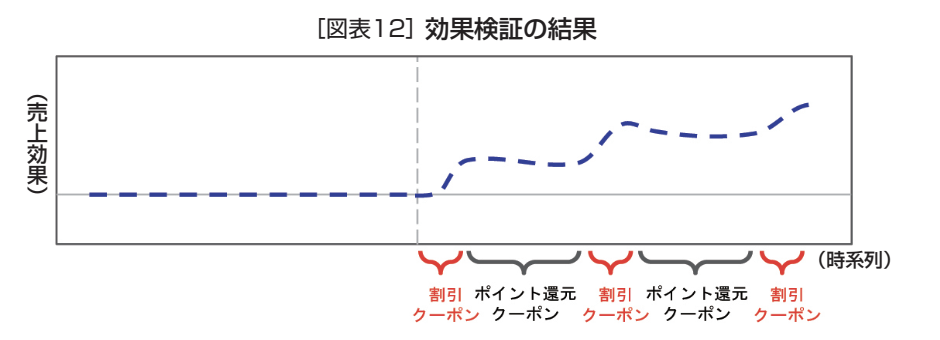
これにより、還元クーポンが配信され続けた場合と、実際のデータとの比較が行われる。その結果が図表12である。横軸は時系列、縦軸は購入金額（その日時点の累積の売上効果）を示している。これによれば、ポイント還元から割引に切り替わった時点で購入金額は上がっている。

そしてその後、ポイント還元のクーポンが配信されたタイミングで効果の上昇は止まっている。そしてまた割引クーポンが配信されたタイミングで効果は上がって行く。割引クーポンが配信されるタイミングで効果が増えることから、割引の方が効果的であることがわかる。

また、還元クーポンが配信されるタイミングでは効果が増加していない。これは比較している対象が還元クーポンを配信し続けた場合であることから、ある意味当然の結果と言える。そしてそれをしっかりと分析結果として得られていることから、この分析方法の再現性が高いことを示している。的確な分析ができていなければ、ここまで明確なデータは出ない。

「何もしなくても購入した人」への販促を極力減らすことができる

ドラッグストアも大規模化し、メーカーとの共同企画も含め、年間の販促費用は相当な額に達している。この中には「販促しなくても購入した人」への販促（ムダ打ち）も相当含まれている。先に述べたような効果検証を的確に利用すれば、このような販促のムダ打ちが発生している部分を発見し、効果のあった販促だけを残し、さらに成果を積み上げることができる。欧米の大手小売業では既に実際のA/Bテストを多用し、販促効果を正しく検証することで精度を上げている。

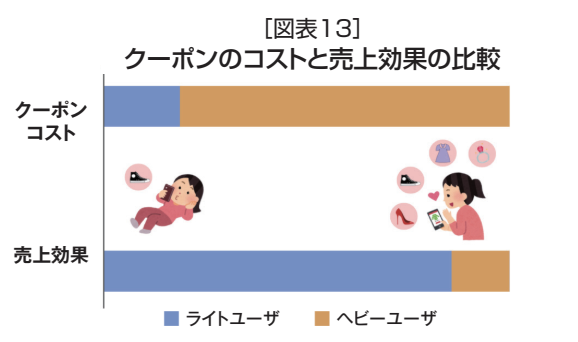
例えば、ユーザーをヘビーユーザーとライトユーザーの二つのセグメントに分割し、それぞれで効果検証を行えば、セグメントごとに販促の効果とコストを捉えることが可能になる。図表13はサイバーエージェントが実際のクーポン施策を分析した、ライトユーザーとヘービーユーザーのクーポンコストと売上効果の比較である。

ヘビーユーザーにコストの大半を費やしているが、売上効果のほとんどはライトユーザーから得られている。サイバーエージェントが効果検証を行ったある小売店では、クーポンのコストを半分以下に減らしてもほぼ同じ効果が得られることがわかった。

ヘビーユーザーはとくに販促を打たなくても、すでに習慣化しているなどの理由から購買する傾向があるのでこのような結果がでる。ヘビーユーザーに限らず、サイバーエージェントが行った効果検証を見ると、販促のムダ打ちは実は多い。これは、セレクションバイアスを可能な限り除去して効果検証することの重要性を物語っている。

例えば、年間1億円の販促費を使っているとして、仮に50％のムダ打ちが生じているとすれば、5,000万円が浪費されていることになる。そして、不正確な効果検証のままでは、莫大な費用が「何もしなくても購入した人」へと費やされ続けるのである。

これを改めれば相当のムダ打ちを是正することが可能で、その分、潤沢な資金が残る。その資金を正確な効果検証で明らかになった効果の高い販促に再投資すればさらに大きな売上へとつながるのである。

 

《取材協力》